

Stephen Hawking's Epitaph
His formula for the temperature of a Black Holeby Tony Heyes
Stephen Hawking's formula for the temperature of a Black Hole is inscribed on his tombstone in Westminster Abbey and also on one of my tee shirts. My tribute to an old friend.
Stephen was never afraid of an arument and never shy of a controvesy. When in 1972 Jacob Bekenstein suggested that there should be thermodynamics of black holes Stephen was one of his detractors. Subsequent anslysis led to a change of mind after which Stephen persued the subject with enthusiasm.
Stepehen's temperature formula is most remarkable. It is the only formula I know which incorporates both Classical Constants and Quantum Constants.
Actually, Hawking's somewhat similar formula for the Entropy of a Black Hole also does this.
I had always understood that it was this latter formula that Stephen wished to have as his epitaph!

|

|
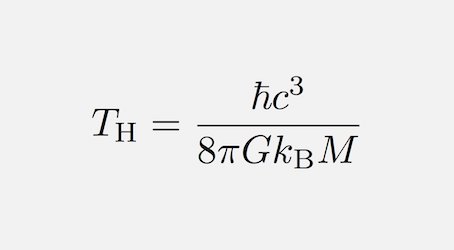
For more information as to the significance of this formula listen to my radio interview
On Stephen Hawking's EpitaphThose, like me, who enjoy doing calculations will need to know the values of the various constants; so here they are:Or watch a video: Deriving Hawking's most famous equation:
The Temperature of a Black Hole
c Velocity of light = 299,792,458 m s-1Given that the above are all constants the temperature equation may be reduced to:h bar Planck's concstant/2pi = 1.05 x 10^-34 kg m2 s-1
pi = 3.14
G Newton's Gravitational constant = 6.67 x 10^-11 m3 kg-1 s-2
kb Boltzmann's constant = 1.38 x 10^-23 m2 kg s-2 K-1
where Ms = the number of solar masses.
Note: the mass of the sun =
1.989 X 10^30 kg
the mass of the moon = 7.347 X 10^22 kg
the Cosmic Microwave Background radiation temperature = 2.725 deg K
the diameter of a Black Hole =
2 X the Schwarzschild radius
= 4GM/c^2 m
Now it is easy to work out the mass of tbe Black Hole whose temperature equals that of tbe Cosmic Background Radiation.
Notice that it is approximately equal to the mass of our Moon and has the diameter of a human hair!
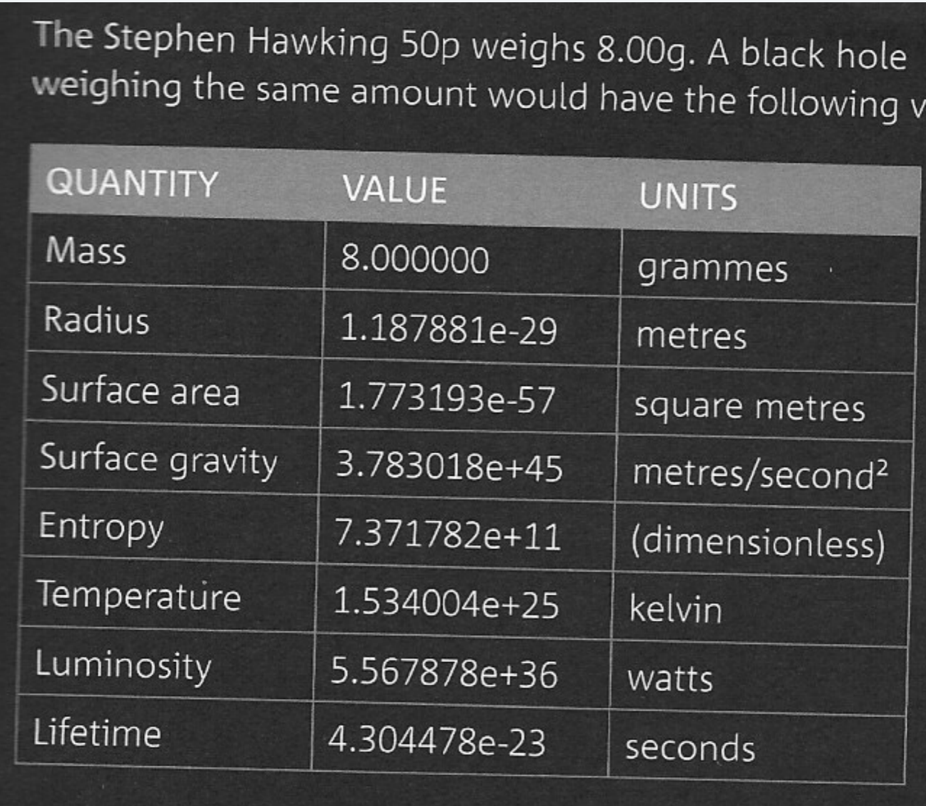
In 2019 the Royal Mint produced a commemorative 50 pence coin to celebrate Stephen's life. The obverse of the coin shows an artist's impressionof a black hole. With tbe aid of a magnifying glass one may also see the Hawking formula for the entropy of a black hole. what a pity the artist did not choose to have a hole in the middle of the coin surrounded by an accretion disk. To avoid making a mess of the Queen's face on the other side the hole could have been a dimple.


In 2015 Stephen delivered the BBC Reith lectures.
I Do Black Holes have no hair?why Stephen, like me, was grateful for Britain's National Health Service
To learn more about Hawking Rradiation read on....
Unsure as to some of the detail (for instance: since Hawking Radiation comes not from within the black hole but from the event horizon, is the intensity of the radiation determined by the temperature of the black hole) I asked ChatGTP about this relationship and received the following answers...
The increase in Hawking radiation with temperature, despite the fact that it depends on the number of virtual particles captured at the event horizon, is fundamentally linked to quantum mechanical principles and the nature of black holes.Higher temperature means that the black hole is smaller and more energetic. In quantum mechanics, higher energy (or higher temperature) corresponds to more intense quantum fluctuations. These fluctuations are responsible for the creation of virtual particle pairs near the event horizon.
Probability of Particle Escape:
Near a hotter (and hence smaller) black hole, the gravitational gradient at the event horizon becomes steeper. This increased gradient enhances the probability that one particle of a virtual particle-antiparticle pair can escape while the other is captured. - Because the black hole is smaller and hotter, the particles that escape have higher average energy, contributing to an increase in the intensity of the Hawking radiation.Energy Spectrum of Radiation:The spectrum of Hawking radiation is thermal, meaning it resembles the radiation from a black body at the corresponding temperature. A higher temperature black hole emits radiation at shorter wavelengths (higher frequencies), which corresponds to higher energy particles.Evaporation and Feedback Loop:
Thus, as the temperature increases, not only does the number of virtual pairs that contribute to Hawking radiation increase, but the radiation itself becomes more intense and energetic.As the black hole emits Hawking radiation and loses mass, it gets smaller, which raises its temperature further. This increase in temperature leads to even more intense radiation, creating a feedback loop that accelerates the evaporation process.And finally a photograph taken I tbe 60s at the time I knew Stephan and Jane.
